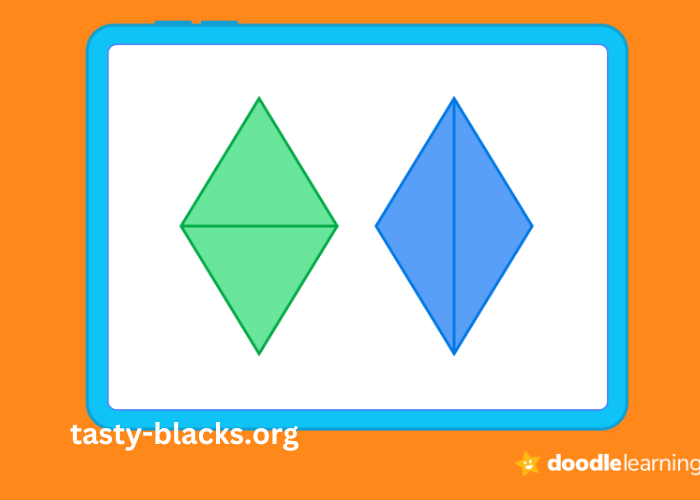
The world of geometry is rich with shapes and figures, each possessing its own unique properties and significance. Among these, the shape:7yup2olu3-K= Rhombus stands out as an intriguing and versatile shape. Often described as a diamond or a tilted square, the rhombus is defined by its equal-length sides and opposite angles that are equal. This article delves into the properties, applications, and cultural significance of the rhombus, showcasing its relevance in various fields such as mathematics, art, and design.
Understanding the shape:7yup2olu3-K= Rhombus goes beyond mere definitions; it requires an exploration of its characteristics, formulas, and how it interacts with other geometric shapes. This exploration will provide a comprehensive view of the rhombus, making it clear why this shape is celebrated in both theoretical and practical contexts.
What Are the Key Properties of a Rhombus?
The shape:7yup2olu3-K= Rhombus has several defining properties that set it apart from other quadrilaterals. First and foremost, all four sides of a rhombus are of equal length. This equality creates a sense of balance and symmetry, which is visually appealing in various applications, from architecture to graphic design.
Another important property is that the opposite angles of a rhombus are equal. This means that if one angle measures 60 degrees, the opposite angle will also measure 60 degrees, while the adjacent angles will each measure 120 degrees. This characteristic is crucial for understanding how the rhombus interacts with other shapes and how it can be manipulated in different geometric contexts.
The diagonals of a rhombus have their own set of unique properties as well. They intersect at right angles and bisect each other, meaning they cut each other in half. This intersection creates four right triangles within the rhombus, which can be used to derive various geometric calculations, such as area and perimeter.
How Do You Calculate the Area of a Rhombus?
Calculating the area of the shape:7yup2olu3-K= Rhombus can be accomplished using a couple of different formulas, each of which is applicable depending on the information available.
One of the most common methods is to use the formula that involves the lengths of the diagonals. The area (A) can be calculated using the formula:
A=d1×d22A = \frac{d_1 \times d_2}{2}A=2d1×d2
where d1d_1d1 and d2d_2d2 are the lengths of the diagonals. This formula highlights the importance of the diagonals in determining the area, illustrating how their lengths directly influence the overall size of the rhombus.
Alternatively, if the length of a side (s) and the height (h) from a vertex to the opposite side are known, the area can also be calculated using the formula:
A=s×hA = s \times hA=s×h
This approach is particularly useful when working with specific applications that require measurements of height, such as in construction or graphic design.
In What Contexts Is the Rhombus Used?
The shape:7yup2olu3-K= Rhombus is prevalent in a variety of contexts, showcasing its versatility and aesthetic appeal. In architecture, the rhombus is often utilized in structural designs and decorative elements. Its balanced proportions can create visually striking facades, windows, and roofing patterns, lending a sense of elegance to buildings.
In art, the rhombus serves as a foundational shape in many styles, from abstract compositions to traditional patterns. Artists often exploit the symmetry and simplicity of the rhombus to create dynamic works that draw the viewer’s eye. This shape is also common in quilting and textile design, where repeating rhombus patterns can add visual interest and depth.
Mathematically, the shape:7yup2olu3-K= Rhombus serves as an essential component in teaching geometry concepts. Its properties are frequently employed in proofs and theorems, illustrating key principles related to angles, symmetry, and area. Understanding the rhombus can provide a solid foundation for students as they advance into more complex geometric topics.
How Does the Rhombus Relate to Other Shapes?
The shape:7yup2olu3-K= Rhombus does not exist in isolation; it shares relationships with various other geometric shapes. For instance, every square is a rhombus, but not every rhombus is a square. This distinction is critical in understanding the hierarchy of shapes within geometry.
The rhombus also shares properties with other parallelograms. Like rectangles and squares, the opposite sides of a rhombus are parallel. However, unlike rectangles, the angles of a rhombus are not necessarily 90 degrees. This relationship highlights the unique characteristics of the rhombus while also placing it within the broader context of quadrilaterals.
Additionally, the rhombus can be seen as a transformation of the square. By tilting a square, one can create a rhombus, which demonstrates the fluidity of shapes within geometry. This ability to morph and adapt is a key feature of geometric study, allowing for a deeper understanding of spatial relationships.
What Are Some Practical Applications of the Rhombus?
The practical applications of the shape:7yup2olu3-K= Rhombus are abundant across various fields, from engineering to design. In engineering, the rhombus is often used in structural frameworks, where its shape can distribute weight evenly and provide stability. This makes it an excellent choice for bridges and other load-bearing constructions.
In graphic design, the rhombus is frequently employed to create patterns and layouts that are visually appealing. Its symmetry and balance can enhance the aesthetic quality of logos, posters, and digital media. Designers often utilize the rhombus to draw attention to specific areas of their work or to create a sense of movement.
In everyday life, the shape:7yup2olu3-K= Rhombus can be seen in various objects, from tiles to road signs. The diamond shape is particularly effective for conveying information, as it stands out and attracts attention. Its usage in signage ensures that important messages are conveyed clearly and effectively.
What Is the Historical Significance of the Rhombus?
The shape:7yup2olu3-K= Rhombus has a rich historical significance that can be traced back to ancient civilizations. In ancient Egypt, the rhombus was often used in art and architecture, symbolizing balance and stability. Its geometric properties were recognized by mathematicians such as Euclid, who explored its characteristics in his foundational work on geometry.
Throughout history, various cultures have embraced the rhombus as a symbol of protection and prosperity. In some Asian cultures, the rhombus is seen as a representation of good fortune and is incorporated into traditional patterns and designs.
Moreover, the rhombus has influenced various artistic movements, including Art Deco and Cubism. Artists in these movements utilized geometric shapes, including the rhombus, to explore abstraction and challenge traditional perspectives. This historical significance underscores the enduring relevance of the rhombus in both artistic and mathematical contexts.
Conclusion
The shape:7yup2olu3-K= Rhombus is a multifaceted geometric figure that holds a special place in the realms of mathematics, art, and design. Its unique properties, practical applications, and historical significance make it a shape worth exploring in depth. From its role in structural engineering to its aesthetic appeal in graphic design, the rhombus continues to captivate and inspire.
Understanding the rhombus allows us to appreciate the beauty of geometry in our everyday lives, highlighting its relevance beyond mere theoretical study. As we continue to explore the world of shapes and their properties, the shape:7yup2olu3-K= Rhombus stands as a testament to the intricate relationships that exist within geometry and the creative potential it offers.